Evaluation of an Expression

Memory limit: 128 MB

Consider an expression 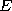, containing integer constants from 0 to 9, variables from to , and the following operations: addition, multiplication and exponentiation with a constant exponent. Quite surprisingly, each of the variables 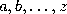appears in the expression 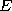at most once. For a given prime number 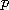, we would like to know how many roots modulo 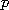the polynomial represented by this expression has. In other words, we want to count the number of ways in which integers from 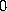to 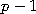can be assigned to the variables in 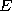, so that the value of 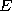is divisible by 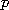. Since the number of such roots can turn out large, it suffices to output it modulo .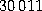

For example, the polynomial represented by the following expression:

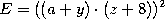
has 15 roots modulo 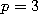, among which the roots:

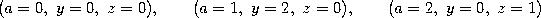
can be found.

More formally, an expression is defined as follows:

• Each integer constant 0, 1, ..., 9 is an expression.
• Each variable a, b, ..., z is an expression.
• If A and B are any expressions, then each of (A+B) and (A*B) is also an expression: the first is the sum of expressions A and B, and the second is their product.
• If A is any expression, and B is an integer constant from 2, 3, ..., 9, then (A^B) is also an expression: the expression A raised to the power of B.

Input

The first line of input contains one prime number 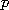(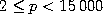). The second line contains an expression 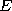as specified above, described by a sequence of at most 300 characters 0, 1, ..., 9, a, b, ..., z, +, *, ^, (, ), without any white space.

Output

Let 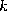denote the number of roots modulo 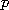of the polynomial 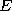. Your program should output one non-negative integer, .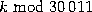

Example

For the input data:

3
(((a+y)*(z+8))^2)

the correct result is:

15

Task author: Jakub Radoszewski.